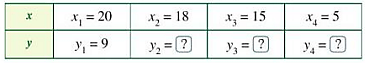Mục lục Giải bài tập Toán 7 Bài 8: Đại lượng tỉ lệ nghịch

Hoạt động khởi động

Khởi động trang 64 Toán lớp 7 Tập 1: Khi tham gia thi công dự án đường cao tốc Nội Bài – Lào Cai, một đội công nhân gồm 18 người dự định hoàn thành công việc được giao trong 12 ngày. Nhưng khi bắt đầu công việc, đội công nhân được bổ sung thêm thành 27 người. Giả sử năng suất lao động của mỗi công nhân là như nhau.

* Khi số công nhân tăng lên thì thời gian hoàn thành công việc sẽ tăng hay giảm đi?

* 27 công nhân hoàn thành công việc đó trong bao lâu?

Lời giải:

• Khi số công nhân tăng lên thì thời gian hoàn thành công việc sẽ giảm đi.

• 1 công nhân hoàn thành công việc trong số ngày là: 12.18 = 216 (ngày)

27 công nhân sẽ hoàn thành công việc trong số ngày là: 216 : 27 = 8 (ngày).

Vậy 27 công nhân hoàn thành công việc đó trong 8 ngày.

1. Khái niệm

Hoạt động 1 trang 64 Toán lớp 7 Tập 1: Giả sử một xe ô tô chuyển động đều trên quãng đường AB dài 240km, Vận tốc v (km/h) và thời gian t (h) của xe ô tô khi đi từ A đến B được liên hệ theo công thức v = $\frac{240}{t}$. Tìm số thích hợp cho $\boxed{?}$ trong bảng sau: 

Lời giải:

Ta có: v = $\frac{240}{t}$

+) Thay t = 3 ta được $v=\frac{240}{3}=80$ (km/h)

+) Thay t = 4 ta được $v=\frac{240}{4}=60$ (km/h)

+) Thay t = 5 ta được $v=\frac{240}{5}=48$ (km/h)

+) Thay t = 6 ta được $v=\frac{240}{6}=40$ (km/h)

Ta có bảng sau:

a) Gọi x (h) là thời gian người công nhân đó làm và y là số sản phẩm làm được trong 1 giờ. Viết công thức tính y theo x.

b) Hỏi x và y có phải là hai đại lượng tỉ lệ nghịch hay không? Nếu có hãy xác định hệ số tỉ lệ.

c) Tính giá trị của y khi x = 10; x = 20; x = 25.

Lời giải:

a) Công thức tính y theo x là: y = $\frac{1000}{x}$.

b) Vì khi x tăng thì y giảm và y liên hệ với x theo công thức y = $\frac{a}{x}$ với a = 1000.

c) Ta có: y = $\frac{1000}{x}$.

+) Thay x = 10 ta được y = $\frac{1000}{10}=100$

+) Thay x = 20 ta được y = $\frac{1000}{20}=50$

+) Thay x = 25 ta được y = $\frac{1000}{25}=40$.

2. Tính chất

Hoạt động 2 trang 65 Toán lớp 7 Tập 1: Cho biết x, y là hai đại lượng tỉ lệ nghịch với nhau: 

a) Hãy xác định hệ số tỉ lệ.

b) Tìm số thích hợp cho $\boxed{?}$ trong bảng trên.

c) So sánh các tích: x₁.y₁; x₂.y₂; x₃.y₃; x₄.y₄.

d) So sánh các tỉ số: $\frac{x_1}{x_2}$ và $\frac{y_2}{y_1}$;$\frac{x_1}{x_3}$ và $\frac{y_3}{y_1}$; $\frac{x_3}{x_4}$ và $\frac{y_4}{y_3}$.

Lời giải:

a) Vì x và y là hai đại lượng tỉ lệ nghịch với nhau nên xy = a

Có x₁ = 20; y₁ = 9 ta được: a = 20.9 = 180.

Vậy xy = 180 và hệ số tỉ lệ nghịch là a = 180.

b) Theo câu a ta có x.y = 180 nên $y=\frac{180}{x}$ 

+) Thay x₂ = 18 ta được y₂ = $\frac{180}{18}=10$

+) Thay x₃ = 15 ta được y₃ = $\frac{180}{15}=12$

+) Thay x₄ = 5 ta được y₄ = $\frac{180}{5}=36$

Ta có bảng sau:

Luyện tập 2 trang 66 Toán lớp 7 Tập 1: Một ô tô dự định đi từ A đến B trong 6 giờ. Nhưng thực tế ô tô đi với vận tốc gấp $\frac{4}{3}$ vận tốc dự định. Tính thời gian ô tô đã đi quãng đường AB.

Lời giải:

Gọi t (giờ) là thời gian ô tô đã đi (t > 0).

Vì vận tốc thực tế gấp $\frac{4}{3}$ vận tốc dự định nên tỉ lệ giữa vận tốc thực tế và vận tốc dự định là $\frac{4}{3}$.

Mà vận tốc và thời gian là hai đại lượng tỉ lệ nghịch với nhau nên tỉ lệ thời gian dự định với thời gian thực tế là $\frac{3}{4}$.

Ta có: $\frac{t}{6}=\frac{3}{4}$

Do đó: t = $\frac{6.3}{4}=\mathrm{4,5}$(giờ) = 4 giờ 30 phút

Vậy thời gian ô tô đã đi thực tế là 4 giờ 30 phút.

3. Một số bài toán

Luyện tập 3 trang 67 Toán lớp 7 Tập 1: Một xưởng may có 56 công nhân dự định hoàn thành công việc trong 21 ngày. Nhưng bên đặt hàng muốn nhận hàng sớm nên xưởng may cần phải hoàn thành hợp đồng trong 14 ngày. Hỏi xưởng may cần phải tăng thêm bao nhiêu công nhân? Giả sử năng suất lao động của mỗi người là như nhau.

Lời giải:

Gọi x (công nhân), y (ngày) lần lượt là số công nhân và thời gian đội sản xuất hoàn thành hợp đồng tương ứng (x ∈ ℕ*, y > 0).

Khi đó, mối quan hệ giữa số công nhân (x) và thời gian hoàn thành hợp đồng (y) là hai đại lượng tỉ lệ nghịch với nhau.

Giả sử số công nhân đang có là x1 = 56, dự định hoàn thành hợp đồng trong y1 = 21 (ngày)

Số công nhân cần có là x2 để hoàn thành hợp đồng trong y2 = 14 (ngày)

Áp dụng tính chất tỉ lệ nghịch ta có:

x₁.y₁ = x₂.y₂

Thay x₁ = 56; y₁ = 21; y₂ = 14 ta có:

56.21 = 14. x₂

Suy ra $x_2=\frac{56.21}{14}=84$ (công nhân)

Số công nhân mà xưởng may cần tăng thêm là:

84 – 56 = 28 (công nhân).

Vậy xưởng may cần bổ sung 28 người để hoàn thành hợp đồng như dự định.

Luyện tập 4 trang 67 Toán lớp 7 Tập 1: Có ba bánh răng a, b, c ăn khớp nhau (Hình 13).

Số răng của mỗi bánh răng a, b, c theo thứ tự là 24; 18; 12. Cho biết mỗi phút bánh răng c quay được 18 vòng. Tính số vòng quay trong một phút của mỗi bánh răng a và b.

Lời giải:

Gọi x; y; z là số vòng mà mỗi bánh răng quay được trong mỗi phút (x; y; z > 0)

Vì số răng của bánh răng tỉ lệ nghịch với số vòng quay được trong một phút nên ta có:

24.x = 18.y = 12.z

Mà z = 18 nên 24.x = 18.y = 12.18

Hay 24.x = 18.y = 216

Ta có:

• 24.x = 216 suy ra $x=\frac{216}{24}=9$ (vòng)

• 18.y = 216 suy ra $y=\frac{216}{18}=12$ (vòng)

Vậy số vòng quay mỗi phút của mỗi bánh răng a và b là 9 vòng và 12 vòng.

Bài tập

Bài 1 trang 68 Toán lớp 7 Tập 1: Giá trị của hai đại lượng x; y được cho bởi bảng sau:  

Hai đại lượng x và y có tỉ lệ nghịch với nhau không? Vì sao?

Lời giải:

Ta có:

x₁.y₁ = 3.32 = 96;

x₂.y₂ = 4.24 = 96;

x₃.y₃ = 6.16 = 96;

x₄.y₄ = 8.12 = 96;

x₅.y₅ = 48.2 = 96.

Vì x₁.y₁ = x₂.y₂ = x₃.y₃ = x₄.y₄ = x₅.y₅ = 96 nên hai đại lượng x và y tỉ lệ nghịch với nhau.

Bài 2 trang 68 Toán lớp 7 Tập 1: Cho biết x; y là hai đại lượng tỉ lệ nghịch với nhau và khi x = 36 thì y = 15.

a) Tìm hệ số tỉ lệ.

b) Viết công thức tính y theo x.

c) Tính giá trị của y khi x = 12; x = 18; x = 60.

Lời giải:

a) Vì x và y là hai đại lượng tỉ lệ nghịch với nhau nên hệ số tỉ lệ là:

a = $x_1{y}_1$ = 36.15 = 540.

b) Vì y và x là hai đại lượng tỉ lệ nghịch với nhau theo hệ số tỉ lệ a = 540 nên công thức tính y theo x là: y = $\frac{540}{x}$.

c) Theo câu b) công thức tính y theo x là: y = $\frac{540}{x}$.

Thay x = 12 ta được y = $\frac{540}{12}$ = 45;

Thay x = 18 ta được y = $\frac{540}{18}$ = 30;

Thay x = 60 ta được y = $\frac{540}{60}$ = 9.

Bài 3 trang 68 Toán lớp 7 Tập 1: Theo dự định, một nhóm thợ có 35 người sẽ xây một tòa nhà hết 168 ngày. Nhưng khi bắt đầu làm, có một số người không tham gia được nên nhóm thợ chỉ còn 28 người. Hỏi khi đó nhóm thợ phải mất bao nhiêu lâu để xây xong tòa nhà? Giả sử năng suất làm việc của mỗi người như nhau.

Lời giải:

Gọi x (người) và y (ngày) là số người thợ và số ngày để xây hết một tòa nhà (x ∈ ℕ*; y > 0).

Vì số người thợ và số ngày xây nhà tỉ lệ nghịch với nhau nên: x₁.y₁ = x₂.y₂.

Thay x₁ = 35; y₁ = 168; x₂ = 28 ta được:

35.168 = 28.y₂

Suy ra $y_2=\frac{35.168}{28}=210$ (ngày)

Vậy 28 người thợ thì phải xây 210 ngày để xong tòa nhà.

Bài 4 trang 68 Toán lớp 7 Tập 1: Chị Lan định mua 10 bông hoa với số tiền định trước. Nhưng do vào dịp lễ nên giá hoa tăng 25%. Hỏi với số tiền đó, chị Lan sẽ mua được bao nhiêu bông hoa.

Lời giải:

Vì giá hoa tăng lên 25% nên giá hoa mới sẽ bằng 125% giá hoa gốc

Do đó giá hoa mới bằng $\frac{5}{4}$ giá hoa gốc.

Gọi số bông hoa mà chị Lan sẽ mua được là x (bông).

Vì số bông hoa mua được tỉ lệ nghịch với giá tiền một bông hoa nên tỉ số của số bông hoa mua thực tế với số bông hoa mua dự định là $\frac{4}{5}$.

Do đó ta có: $\frac{x}{10}=\frac{4}{5}$.

Vậy số hoa mà chị lan mua được là: x = $\frac{10.4}{5}=8$ (bông)

Vậy chị Lan sẽ mua được 8 bông hoa.

Bài 5 trang 68 Toán lớp 7 Tập 1: Ở nội dung bơi 400m nữ tại vòng loại Thế vận hội mùa hè năm 2016, vận động viên Nguyễn Thị Ánh Viên đã về đích với thành tích 4 phút 36 giây 85(tức là 4 phút và 36,85 giây).

(Nguồn: https://vi.wikipedia.org)

Cũng ở nội dung bơi 400m nữ tại Giải bơi lội vô địch thế giới tổ chức ở Kazan (Nga) năm 2015, Ánh Viên đạt thành tích là 4 phút 38 giây 78 (tức là 4 phút và 38,78 giây).

(Nguồn: https://cand.com.vn)

Tính tỉ số giữa tốc độ bơi trung bình của Ánh Viên tại Thế vận hội mùa hè năm 2016 và tại Giải bơi vô địch thế giới tổ chức ở Kazan (Nga) năm 2015.

Lời giải:

Đổi 4 phút 36,85 giây = 276,85 giây;

Đổi 4 phút 38,78 giây = 278,78 giây.

Tỉ số giữa thời gian bơi của Ánh Viên tại Thế vận hội mùa hè năm 2016 và Giải bơi vô địch thế giới tổ chức ở Kanzan (Nga) năm 2015 là: $\frac{276,85}{278,78}=\frac{27685}{27878}$

Vì tốc độ bơi và thời gian bơi tỉ lệ nghịch với nhau nên tỉ số tốc độ bơi trung bình của Ánh Viên tại thế vận hội mùa hè năm 2016 với giải bơi vô địch thế giới tổ chứ wor Kazan (Nga) năm 2015 là: $\frac{278078}{276085}$

Bài 6 trang 68 Toán lớp 7 Tập 1: Một loại tàu cao tốc hiện nay ở Nhật Bản có thể di chuyển với tốc độ trung bình là 300km/h nhanh gấp 1,43 lần so với thế hệ tàu cao tốc đầu tiên.

(Nguồn: https:// www.mt.gov.com)

Nếu tàu cao tốc loại đó chạy một quãng đường trong 4 giờ thì tàu cao tốc thế hệ đầu tiên sẽ phải chạy quãng đường đó trong bao nhiêu giờ.

Lời giải:

Vận tốc tàu cao tốc cũ là:

300:1,43 = 209,79 (km/h)

Quãng đường tàu cao tốc mới chạy trong 4 giờ là:

300.4 = 1200 (km)

Thời gian tàu cao tốc cũ chạy trên con đường đó là:

1200: 209,79 = 5,72 (giờ)

Vậy tàu cao tốc cũ chạy trên con đường đó sẽ hết 5,72 giờ.

Bài 7 trang 68 Toán lớp 7 Tập 1: Một bánh răng có 40 răng, quay mỗi phút được 15 vòng, nó khớp với một bánh răng thứ hai. Giả sử bánh răng thứ hai quay một phút được 20 vòng. Hỏi bánh răng thứ hai có bao nhiêu răng.

Lời giải:

Gọi x (số răng) và y (vòng quay) lần lượt là số răng và số vòng quay của bánh răng (x ∈ ℕ*; y > 0).

Vì số vòng quay và số răng của bánh răng tỉ lệ nghịch với nhau nên x tỉ lệ nghịch với y.

Áp dụng tính chất tỉ lệ nghịch ta có:

x₁.y₁ = x₂.y₂.

Vì bánh răng thứ nhất có 40 răng và mỗi phút quay được 15 vòng nên x₁ = 40; y₁ = 15.

Với x₁ = 40; y₁ = 15; y₂ = 20 ta được:

40.15 = 20.x₂

Suy ra $x_2=\frac{40.15}{20}=30$

Vậy bánh răng thứ hai có 30 răng.